Balding–Nichols model
| Parameters | 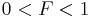 (real) (real)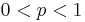 (real) (real)For ease of notation, let 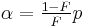 , and , and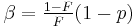 |
|---|---|
| Support | 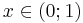 |
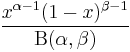 |
|
| CDF | 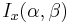 |
| Mean | 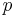 |
| Median | 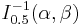 no closed form no closed form |
| Mode | 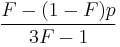 |
| Variance | 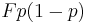 |
| Skewness | 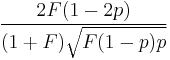 |
| MGF | 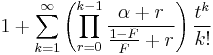 |
| CF | 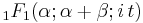 |
In population genetics, the Balding–Nichols model is a statistical description of the allele frequencies in the components of a sub-divided population. With background allele frequency p the allele frequencies, in sub-populations separated by Wright's FST F, are distributed according to independent draws from
where B is the Beta distribution. This distribution has mean p and variance Fp(1 – p).[1]
The model is due to David Balding and Richard Nichols and is widely used in the forensic analysis of DNA profiles and in population models for genetic epidemiology.
References
- ^ Alkes L. Price, Nick J. Patterson, Robert M. Plenge, Michael E. Weinblatt, Nancy A. Shadick & David Reich (2006). "Principal components analysis corrects for stratification in genome-wide association studies" (PDF). Nature Genetics 38 (8): 904–909. doi:10.1038/ng1847. PMID 16862161. http://genepath.med.harvard.edu/~reich/Price%20et%20al.pdf.
|
|||||||||||||||||||||||